Unfortunately the illustrations in the article got corrupted, here they are:
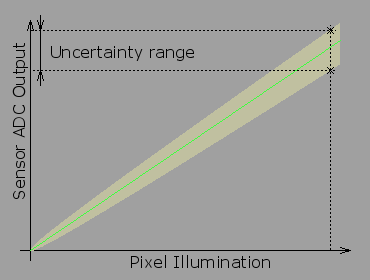
Pixel output uncertainty caused by the shot noise
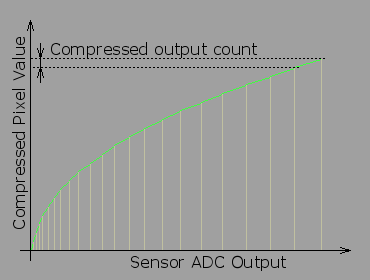
Non-linear conversion of the sensor output
The content below is downloaded from linuxdevices.io/how-many-bits-are-really-needed-in-the-image-pixels/, copyright(s) of the source apply.